Развитие пространственного воображения
0 руб.
0 товар(ов)
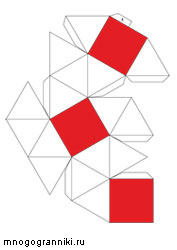
Плосконосый (курносый) куб
Плосконосый (курносый) куб - полуправильный выпуклый многогранник, обладающий двумя свойствами:
1. Все грани являются правильными многоугольниками двух типов - треугольник и квадрат;
2. Для любой пары вершин существует симметрия многогранника (то есть движение, переводящее многогранник в себя) переводящая одну вершину в другую.
Плосконосый (курносый) куб является одним из 13 тел Архимеда.
Архимедовы тела являются полуправильными многогранниками в том смысле, что их грани - правильные многоугольники, но они не одинаковы при этом сохраняется условие одного из типов пространственной симметрии: тетраэдрического, октаэдрического или икосаэдрического.
Многогранник может быть изготовлен в одном из друх вариантов - плосконосый куб, имеющий закрутку влево и имеющий закрутку вправо.
плосконосый куб закрученный влево
плосконосый куб закрученный вправо
Для сборки плосконосого куба закрученного влево потребуется распечатать две развёртки на листах формата А4. Две части развёртки соединяем в единую развёртку как показано на рисунке: Далее склеиваем развёртку и получаем многогранник плосконосый куб.
Развертка многогранника, закрученного вправо
Популярное
Бывают совпадения, о которых мы даже сами не подозреваем. 12 апреля - День Космонавтики!
Нечасто удается встретить многогранники за пределами учебников математики. И если такие геометрические формы как куб, призма и цилиндр встречаются повседневно, то...
Создатели нового браузера* Атом – выбрали для своего логотипа изображение многогранника – икосаэдра. * - программа для просмотра интернет страниц.
Статья в журнале «Наука и Жизнь» рассказывает о достаточно необычном способе построения многогранников.
Раздел геометрии, в котором изучаются фигуры в пространстве именуется стереометрия. Происхождение слова стереометрия относится к Древней Греции – от слов «stereos» —...
Монумент «Звезда Кеплера» (норв. Keplerstjernen), высотой 45 метров, расположен недалеко от города Осло (Норвегия) в окрестностях аэропорта...
Эта модель многогранника представляет из себя пересечение трёх параллелепипедов. В её основе пересечение трёх прямоугольников, где...
