0 руб.
0 товар(ов)
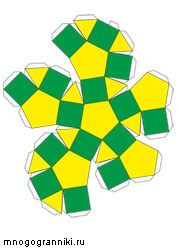
Усечённый икосо-додекаэдр
Усечённый икосо-додекаэдр - полуправильный выпуклый многогранник, обладающий двумя свойствами:
1. Все грани являются правильными многоугольниками трёх типов - пятиугольник, четырехугольник и треугольник;
2. Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую.
Усечённый икосо-додекаэдр является одним из 13 тел Архимеда.
Архимедовы тела являются полуправильными многогранниками в том смысле, что их грани - правильные многоугольники, но они не одинаковы при этом сохраняется условие одного из типов пространственной симметрии: тетраэдрического, октаэдрического или икосаэдрического.
Для сборки усечённого икосо-додекаэдра потребуется распечатать две развёртки на листах формата А4. Две части развёртки соединяем в единую развёртку как показано на рисунке: Далее слеиваем развёртку и получаем многогранник усечённый икосо-додекаэдр
Развертка
Популярное
Это новый, весьма необычный способ создать модель Звёздчатого многогранника открытого 1619 году немецким...
АРХИМЕД (287 - 212 до н.э.) - древнегреческий математик, физик и механик. Архимед - автор многочисленных открытий и...
Можно ли разрезать треугольник на такое количество частей, чтобы из них можно было сложить квадрат?
Лето – это время, которое хочется провести вне помещения. За парту дети сядут в сентябре, а сейчас – все на детскую...
Статья в журнале «Наука и Жизнь» (1989 № 6 А.Черенков, В.Храмов) рассказывает о достаточно...
Во второй половине XIX века в школах США зародился новый способ обучения – метод проектов.Согласно этому подходу истинным и ценным...
До сих пор мы активно применяли для сборки многогранников из наборов «Волшебные грани» клей. Более того,...
