Развитие пространственного воображения
0 руб.
0 товар(ов)
Усеченная восьмиугольная пирамида
В основании пирамиды - правильный восьмиугольник (все стороны которого равны, углы между сторонами составляют 135 градусов).
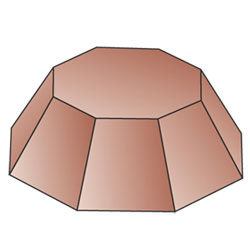
данную пирамиду можно вписать в усечённый конус с радиусами оснований r=35 мм и R=55 мм
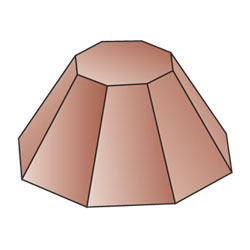
данную пирамиду можно вписать в усечённый конус с радиусами оснований r=25 мм и R=50 мм
данную пирамиду можно вписать в усечённый конус с радиусами оснований r=20 мм и R=50 мм
Популярное
АРХИМЕД (287 - 212 до н.э.) - древнегреческий математик, физик и механик. Архимед - автор многочисленных открытий и изобретений: машины для...
Испанский художник Okuda создал в Москве яркую скульптуру в форме звезды.
1. Вы хотели бы увидеть, как можно преобразовать развертку обычного куба? Если да, то следующий...
Достаточно часто возникает вопрос о практическом применении бумажных развёрток. Какой смысл в бумажном моделировании?
Звезда — это образ божественной идеи, божественной воли, согласно которой возник и начал вращаться в Пространстве и жить наш Свет, Мир.
Для Вашего удобства мы снизили стоимость доставки наборов "Волшебные грани" в разы!
Когда мы готовили 36-ой выпуск «Волшебные грани», у наших коллег возник вопрос: «Почему мы опять собираемся говорить о правильных многогранниках,...
