Развитие пространственного воображения
0 руб.
0 товар(ов)
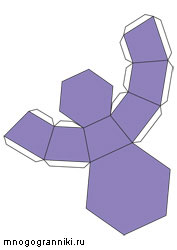
Усеченная шестиугольная пирамида
В основании пирамиды - правильный шестиугольник (все стороны которого равны, углы между сторонами составляют 120 градусов).
данную пирамиду можно вписать в усечённый конус с радиусами оснований r=35 мм и R=55 мм
Популярное
У каждого из пяти тел Платона можно определить следующие математические характеристики: 1. Радиус сферы описанной вокруг многогранника; 2. Радиус сферы...
Предположим, вы впервые увидели на прилавке книжного магазина или на страницах в интернете издание «Волшебные грани». Хочется попробовать? Но вот вопрос, какой выпуск взять на пробу....
Многогранники могут стать украшением вашего дома, создав изюминку в интерьере.
Итальянская компания BULGARI (Булгари), основанная в 1884 году, активно использует в рекламных целях геометрическую форму восьмиугольника для...
Какое из известных нам геометрических тел обладает наибольшей прочностью? Наиболее устойчиво к внешним деформациям?
В этой статье мы постараемся ответить на вопрос: «Можно ли купить для класса Волшебные грани используя бюджетные средства»?
Один из самых известных в нашей стране журналов - популяризаторов науки опубликовал на своих страницах материал об издании «Волшебные грани».
