

Развитие пространственного воображения
0 руб.
0 товар(ов)
Шесть коробочек и золотое сечение
Лука Пачоли в 1509 году, современник и друг Леонардо да Винчи, издал книгу «О божественной пропорции». Пачоли нашел в пяти Платоновых телах – правильных многогранниках (тетраэдр, куб, октаэдр, икосаэдр и додекаэдр) тринадцать проявлений «божественной» пропорции». В главе «О двенадцатом, почти сверхъестественном свойстве» он рассматривает правильный икосаэдр. Если соединить между собой любые два противоположных ребра икосаэдра, получится прямоугольник, у которого большая сторона так относится к меньшей, как сумма сторон к большей. В икосаэдре три пары противоположных ребер образуют три пересекающихся прямоугольника. Соотношение сторон каждого прямоугольника – длина к ширине соответствует значению 1,618 (пропорция золотого сечения).



Модель трех пересекающихся золотых прямоугольников могла бы быть весьма интересна с точки зрения дизайна. Но чтобы создать такую модель в реальном мире прямоугольники должны обладать не только длиной и шириной, но и высотой (или толщиной).
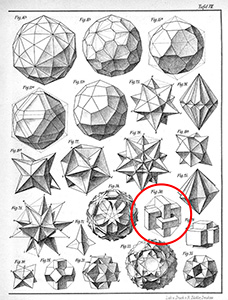
Первую иллюстрацию такой модели мы находим в книге немецкого геометра Макса Брюкнера (1860 – 1934 гг).

Книга «Многоугольники и многогранники: теория и история», издана в Лейпциге в 1900 году. В ней впервые опубликован рисунок модели многогранника, в основе которого лежит пересечение трёх золотых прямоугольников.
Создание модели
Такую модель мы вполне можем изготовить.
Физически – эта модель, представляет из себя, пересечение трёх параллелепипедов (трёх коробочек).
Сторона параллелепипеда имеет пропорции золотого сечения.
Чтобы приступить к созданию модели, нам остается только задать толщину.
Мы будем выбирать размеры из следующих соображений:
1. Сборка модели должна быть предельно простой.
2. Развёртка (или развёртки) должны умещаться на листе стандартного формата.
Зададим следующие размеры параллелепипеда:
- длина = 145,62 мм; (145,62/90 = 1,618 – что соответствует пропорции золотого сечения);
- ширина = 90 мм;
- высота (толщина) = 30 мм.

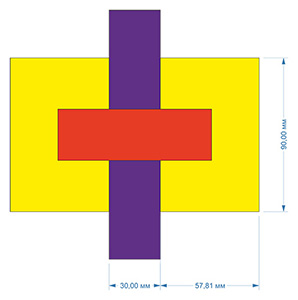
Но как объединить три параллелепипеда в единое тело?
Перед нами стоит задача - максимально упростить конструкцию модели.
У нас есть решение!
Пусть каждый из трех «золотых параллелепипедов» состоит из двух частей. Тогда нам потребуются 3 x 2 = 6 шт. параллелепипедов.
Склеить их между собой не представляет особого труда.

В этом случае размеры «маленьких» параллелепипедов будут составлять:
- ширина (145, 62 – 30) / 2 = 57,81 мм;
- длина = 90 мм;
- высота (толщина) = 30 мм.
Для заданных параметров создаём развертку параллелепипеда.
На одном стандартном листе А4 умещается две таких развертки.
Сборка модели
Для сборки нам потребуются:
- три листа цветной бумаги размером А4 (размер стандартного листа);
- ножницы;
- клей.

1. Распечатайте развёртки на каждом листе.

2. Аккуратно вырежьте развёртки по контуру.
Так как на одном листе мы разместили сразу две развертки, то вырезав развертки с каждого из трёх разноцветных листов, мы получим шесть развёрток.

3. Согните лепестки в местах сгиба.
 4. Склейте лепестки в указанной последовательности.
4. Склейте лепестки в указанной последовательности.


5. Склейте параллелепипеды вместе.






Фокус со спичками.


А если мы немного упростим условие? Пусть наши прямоугольники немного отличаются от пропорций золотого сечения.
– Зачем?
– Из подручных предметов мы сделаем интересную поделку.

Нам потребуются шесть спичечных коробков и клей.
Склеив между собой спичечные коробки в той же последовательности, как и выше, мы получим изящную модель.

Рассматривая модель с точки зрения пересечения трёх прямоугольников, мы получаем пропорцию 1,725 (=88/51). Как видите отклонение от золотого сечения совсем незначительное (всего 6%), а внешний вид очень схожий.

При этом коробочки для спичек не теряют свою функциональность. Спички можно по-прежнему хранить, доставать и использовать.
© mnogogranniki.ru 09/06/2021
Популярное
До сих пор мы активно применяли для сборки многогранников из наборов «Волшебные грани» клей. Более того, настоятельно рекомендовали применять именно клей Супер-ПВА. Есть ли...
Предположим, вы впервые увидели на прилавке книжного магазина или на страницах в интернете издание «Волшебные грани». Хочется попробовать? Но вот вопрос, какой выпуск взять на пробу....
Молодой британский дизайнер Ричард Суини (Richard Sweeney) создает удивительные скульптуры из...
Обработка металла это очень сложный технологический процесс. Но существуют мастера, кто умеет вытачивать многогранники из металла внутри другого...
Архитекторы с древних времен применяли элементы многогранников в создании своих творений. В современно мире этот подход выделяет здания среди тысяч других.
Представьте себе историческое здание, архитектурный ансамбль, который украшают звёздчатые многогранники. И не просто здание, а целый дворец! Возможно ли такое?
В выпуске 25 «Волшебных граней» мы обратили взор читателя на то, что разрезая куб плоскостью, мы получаем в точке разреза сечение, имеющее форму...


