

Развитие пространственного воображения
0 руб.
0 товар(ов)
Мозаика Эшера
Одинаковым узором, повторяющимся на каждой грани многогранника, можно создать чередующуюся комбинацию рисунков на объемном геометрическом теле.
Одним из первых, кто погрузился в изучение свойств симметрии и применении его в искусстве, был голландский художник-график Мауриц Корнелис Эшер.
Эшер известен концептуальными литографиями, гравюрами на дереве и металле, в которых он мастерски иллюстрировал понятия симметрии, бесконечности и особенности психологического восприятия сложных трёхмерных объектов.
Идеи для своих картин Эшер брал из точных наук, из математики и геометрии.
В 1936 году он заинтересовался мозаикой и регулярно использовал ее для заполнения плоскости картины.

Регулярное разбиение плоскости, называемое "мозаикой" - это набор замкнутых фигур, которыми можно замостить плоскость без пересечений фигур и щелей между ними. Обычно в качестве фигуры для составления мозаики используют простые многоугольники, например, квадраты или прямоугольники. Эшер использовал в своих гравюрах все виды мозаик - регулярные и нерегулярные.

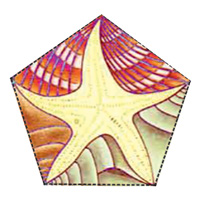
Работа художника "Ракушки и морские звёзды". (Shells and Starfish. 1941 г.).
Математики доказали, что для регулярного разбиения плоскости подходят только три правильных многоугольника: треугольник, квадрат и шестиугольник. Эшер использовал базовые образцы мозаик, применяя к ним трансформации, которые в геометрии называются симметрией, отражение, смещение и др. Также он исказил базовые фигуры, превратив их в животных, птиц, ящериц и проч. Эти искаженные образцы мозаик имели трех-, четырех - и шести-направленную симметрию, таким образом сохраняя свойство заполнения плоскости без перекрытий и щелей.
Используя один из элементов этой мозаики, а именно пятиконечную морскую звезду, по краям касающуюся ракушек, мы можем создать правильный пятиугольник, который послужит гранью додекаэдра.
Здесь вы можете скачать и распечатать на цветном принтере две развёртки для создания додекаэдра:
На фотографиях представлена последовательность сборки додекаэдра (пошаговая инструкция как склеить многогранник из бумаги):
Сначала склейте две части в единую развертку.


Следующим шагом склейте каждую из половинок.


Завершающим этапом склейте между собой две половинки додекаэдра.
Готовый многогранник позволяет увидеть, как пятиугольный рисунок сочетается на двенадцати гранях додекаэдра сам с собой и образует симметричный геометрический узор.

У Маурица Эшера существуют последователи, те кто так же как и он придумывают оригинальные рисунки. Для нас наиболее интересными являются те, что позволяют использовать объемные геометрические формы.
Например, на сайте канадского университета (SFU) были предложены рисунки и развертки для создания пяти правильных многогранников. В качестве повторяющегося мозаичного рисунка использованы образы животных и клоунов:
Используя подобную технику, можно создать яркий и привлекательный образ для каждого из Платоновых тел.

Популярное
Призмы, которые спасли Мир
Сюжет фантастического блокбастера «Пятый элемент», построен на легенде, что существуют пять элементов, которые способны защитить мир от угрозы Абсолютного Зла.
Подарок школьнику за 150 рублей
Найти подарок для школьника, который будет интересным, полезным, а также не разорит семейный бюджет – возможно ли такое в 2020 году? Рассказываем, чем можно...
Правильные многогранники
Правильные многогранники, их всего пять: тетраэдр, октаэдр, куб (другое название гексаэдр),...
Многогранники - предметы интерьера
Многогранники могут стать украшением вашего дома, создав изюминку в интерьере.
Как освоить стереометрию?
Раздел геометрии, в котором изучаются фигуры в пространстве именуется стереометрия. Происхождение слова стереометрия относится к Древней Греции – от слов «stereos» —...









