

Развитие пространственного воображения
0 руб.
0 товар(ов)
Многогранник Силаши - как сделать, развертка
Можно ли создать многогранник, имеющий форму тора (бублик), но с минимальным числом граней?
Предположим, что можно. И сколько же нам потребуется граней?
Кольцо можно получить минимум из трёх граней, но ведь это будут только внутренние грани. А потребуются еще и внешние грани, чтобы это было действительно геометрическое тело.
Как вам задача сделать тороидальный многогранник из семи граней?
Это может показаться невыполнимым. Семь граней слишком мало!
И тем не менее, в 1977 году венгерский математик Лайош Силаши* нашел способ построить тороидальный гептаэдр. Гептаэдр - семигранник. От латинских слов "гепта" - семь и "эдр" - грань.
* Написание фамилии учёного в русском языке встречается в двух вариантах Силаши и Силашши. Сложность связана прежде всего с тем, что произношение в русском языке двойного "ш" на конце слова затруднительно. Родина ученого Венгрия, а венгерский язык считается одним из самых сложных. В оригинале фамилия пишется Szilassi, что, вероятно, ближе к двойному "ш" - Силашши. [1]
 Гептаэдр, топологически эквивалентен тору. Топологически - значит сохраняет свойство тора, даже после видимой деформации.
Гептаэдр, топологически эквивалентен тору. Топологически - значит сохраняет свойство тора, даже после видимой деформации.
 Многогранник Силаши имеет:
Многогранник Силаши имеет:
- 7 граней;
- 14 вершин многогранника;
- 21 ребро.
Что очень порадует любителей нумерологии и числа 7.
И еще и открыт в 77 году XX века.
 Каждая грань многогранника представляет собой шестиугольник (хотя ни один из них не является правильным шестиугольником).
Каждая грань многогранника представляет собой шестиугольник (хотя ни один из них не является правильным шестиугольником).
 У каждой пары граней есть общее ребро многоугольника.
У каждой пары граней есть общее ребро многоугольника.
 Каждая грань многогранника Силаши касается всех остальных граней.
Каждая грань многогранника Силаши касается всех остальных граней.
Другими словами, каждая грань граничит с каждой.
Это, наверное, самое уникальное свойство этого многогранника. Ведь до этого считалось, что только существует только один многогранник, у которого каждая грань граничила с другой. Это был тетраэдр. Но теперь таких многогранников уже 2!
Подробная схема сборки многогранника Силаши.
Часто можно найти такой вариант развертки многогранника Силаши. Развёртка из двух частей:
Но есть две причины, по которым подобного варианта сборки следует избегать.
Первая причина - модель многогранника получается слишком маленькой.
И вторая, наиболее важная, неудобство при сборке. Те, кто предлагает такую развертку, скорее всего никогда не пытались сами изготовить из нее бумажную модель. Если начать сборку с внешнего контура, то аккуратно приклеить внутренние детали потом практически невозможно. Этот вариант развёртки многогранника Силаши можно рассматривать только как вспомогательную инструкцию.
Модель имеет внутреннюю часть с которой очень не просто справиться при сборке.
Мы ставим своей задачей условие, чтобы модель смогли сделать подавляющее большинство читателей. Поэтому предлагаем пойти другим путем. Выбрать размер деталей с которым удобно работать и отказаться от использования развертки в пользу отдельных деталей.
Многогранник содержит 7 деталей. Для каждой потребуется цветной лист бумаги. Но можно сделать и из обычной белой бумаги с последующей самостоятельной окраской кисточкой.
Контуры каждой детали печатаются на цветном листе своего цвета формата А4.
 Если у Вас цветная бумага класса премиум (одна сторона цветная с защитным покрытием), то печатать следует на свободной белой стороне.
Если у Вас цветная бумага класса премиум (одна сторона цветная с защитным покрытием), то печатать следует на свободной белой стороне.
На сборке это никак не отразится, за исключением того момента, что многогранник будет иметь зеркальную симметрию по отношению к исходной схеме.
Готовые детали склеиваются по схеме.
Сначала собираем внутреннюю часть многогранника.




Цветная поверхность деталей должна оказаться внутри, образуя кольцо.
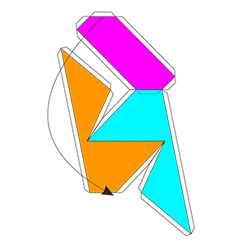

Затем к внутренней части приклеиваем боковые стенки. Зеленая деталь.


Синяя деталь.


Может возникнуть желание склеить между собой синюю и зеленую детали. Но делать этого пока не следует.
Следующим шагом, приклеиваем оставшиеся две боковые детали через лепесток, обозначенный номером 6 для красной детали.


И через лепесток, обозначенный номером 7 для жёлтой детали.

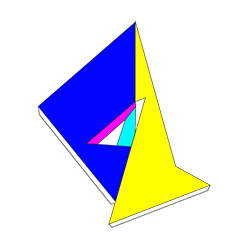
Далее, последовательно приклеиваем свободные лепестки к красной и жёлтой деталям, как указано на схеме:


Завершающим этапом приклеиваем оставшиеся свободные лепестки.
Готовая модель многогранника имеет следующие размеры в мм:

По многочисленным просьбам читателей, мы добавили в статью фотографии со схемой сборки.


Примечания:
1. https://hu.wikipedia.org/wiki/Szilassi_Lajos
© mnogogranniki.ru 21/08/2020
Популярное
Студией Артемия Лебедева (https://www.artlebedev.ru/) была предложена форма скворечника в виде многогранника. В качестве геометрической...
Он круглый, но развёртку деталей для его сборки никто не отменял!
Раздел геометрии, в котором изучаются фигуры в пространстве именуется стереометрия. Происхождение слова стереометрия относится к Древней Греции – от слов «stereos» —...
Знакомые каждому с детства коробочки для Биг-Мака и картошки, стаканчик для Кока-Колы так же делают из бумажных разверток.
Что будет, если плоскую геометрическую фигуру, например прямоугольник, начать быстро вращать относительно одной из его сторон? Одним лишь вращением мы можем...
Почему бумага? Иногда приходится слышать вопрос: «Почему вы выбрали для сборки многогранников такой материал как бумага (или точнее дизайнерский картон)? Это же...




































