Развитие пространственного воображения
0 руб.
0 товар(ов)
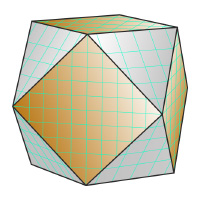
Кубо-октаэдр
Кубооктаэдр - полуправильный выпуклый многогранник, обладающий двумя свойствами:
1. Все грани являются правильными многоугольниками двух типов - треугольник и квадрат;
2. Для любой пары вершин существует симметрия многогранника (то есть движение, переводящее многогранник в себя) переводящая одну вершину в другую.
Кубооктаэдр является одним из 13 тел Архимеда
Архимедовы тела являются полуправильными многогранниками в том смысле, что их грани - правильные многоугольники, но они не одинаковы при этом сохраняется условие одного из типов пространственной симметрии: тетраэдрического, октаэдрического или икосаэдрического.
Радиус описанной сферы кубооктаэдра R=a где a - длина стороны. Напротив, поместить сферу внутрь кубооктаэдра так, чтобы она касалась одновременно всех сторон не удастся. Для выполнения этого условия сфера должна касаться всех квадратов и треугольников. Но расстояния разные. Площадь поверхности кубооктаэдра. Площадь поверхности можно определить по следующей формуле: Объем кубооктаэдра определяется по следующей формуле: Кубооктаэдр можно разделить плоскостью на две равные части. При этом сечение будет иметь форму правильного шестиугольника. Знаменитая математическая задача "О семи кёнигсбергских мостах" или Путь Эйлера может быть переформулирована и рассмотрена на примере ребер кубооктаэдра. Как последовательно обойти все ребра кубооктаэдра? Одного ребра нельзя касаться дважды. На рисунке приведен анимационный пример решения этой задачи. Одно из названий задачи - Путь Эйлера. В честь знаменитого математика Леонарда Эйлера.
Для сборки кубо-октаэдра потребуется распечатать развёртку на обычном листе формата А4. Скачать развёртку. Кроме того, существуют другие варианты окраски многогранника, когда каждая из соседних граней окрашена в свой цвет. Либо используется определенное количество цветов раскраски, причем одинаковые цвета не граничат друг с другом. Представляем Вашему вниманию два варианта окраски кубооктаэдра с использованием пяти цветов.
Математические характеристики кубооктаэдра
Кубооктаэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.
Возможны следующие четыре варианта разреза кубооктаэдра:
Развертки для создания кубооктаэдра
Готовый набор
Популярное
Мы приоткрываем завесу таинства – как производится наша продукция. И сделаем это на примере...
Испанский художник Okuda создал в Москве яркую скульптуру в форме звезды.
Достаточно часто возникает вопрос о практическом применении бумажных развёрток. Какой смысл в бумажном моделировании?
Что будет, если плоскую геометрическую фигуру, например прямоугольник, начать быстро вращать относительно одной из его сторон? Одним лишь вращением мы можем...
Нечасто удается встретить многогранники за пределами учебников математики. И если такие геометрические формы как куб, призма и цилиндр встречаются повседневно, то...
