

Развитие пространственного воображения
0 руб.
0 товар(ов)
-
Вы здесь:
- Главная
- Сечения красного куба
Сечения красного куба

Здесь вы найдете математические задачи, для решения которых этот куб очень удобно использовать в качестве наглядного пособия.
Задача № 1
Сложность 1/5Задание:


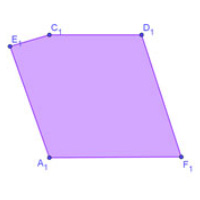
Какой след оставит на бумаге выполненное скульптором сечение?



Решение:
Найдите на имеющемся кубе пятиугольное сечение. Посмотрите на его форму.


Ответ:
Сечение № 1
Задача № 2
Сложность 3/5
Задание:
Современный скульптор, с говорящим псевдонимом Diamond, решил так срезать часть куба, чтобы новая грань была похожа очертаниями на образ бриллианта.

Вопрос:
Как необходимо произвести сечение куба, чтобы в результате сечение имело форму следующего пятиугольника? (Обратите внимание на симметрию пятиугольника). В ответе укажите три точки, необходимые для построения плоскости сечения.
Варианты ответов:
1) D1 C1 F1
2) B2 G2 V1
3) M2 K2 S1
4) S1 Q1 H2
Решение:
Рассмотрите пятиугольное сечение куба. Соотнесите указанные точки на чертеже .

Ответ: 1) D1 C1 F1
Чтобы получить такое сечение надо повернуть куб следующим образом. Далее делаем срез. Получаем в сечении пятиугольник, имеющий очертания бриллианта.

Задача № 3
Сложность 1/5
Задание:
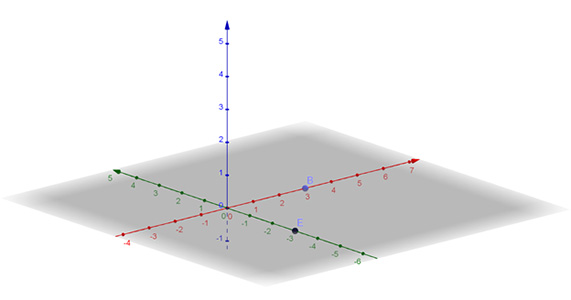
Постройте куб с ребром равным трём единичным отрезкам, и с двумя вершинами в точках E(0,-3,0), B(3,0,0)
Ответ:

Задача № 4
Сложность 1/5
Задание:
Точки A1 и E1 принадлежат рёбрам AB и BC куба ABFEDCGH и имеют следующие координаты: A1 (1,0,0),E1 (3,0,2). Точка К лежит на прямой A1E1. Какой плоскости принадлежит точка К?

Варианты ответов:
1) ABC
2) CGF
3) HGF
Решение:
1. Для визуального удлинения одной из сторон сечения можно воспользоваться методом приложения карандаша к уже имеющемуся изделию. Не забудьте, пожалуйста, верно сопоставить грани Вашей поделки с предлагаемым чертежом.
2. Можем воспользоваться Аксиомой о прямой, принадлежащей плоскости: Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. Точки A1 и E1 принадлежат рёбрам AB и BС, т.е. точки A1 и E1 принадлежат грани ABC, следовательно и вся прямая принадлежит грани ABC, в частности и одна из ее точек K.
Ответ:
1) ABC
Задача № 5
Сложность 1/5
Задание:
Точки A1 и E1 делят рёбра AB и BC куба ABFEDCGH в отношении 1:3.

Вопрос:
По какой прямой пересекаются плоскости BE1F и A1BE1 Варианты ответов:
1) BC
2) HE
3) AB
Решение:
1.Для визуального удлинения одной из сторон сечения можно воспользоваться методом приложения карандаша к уже имеющемуся изделию. Не забудьте, пожалуйста, верно сопоставить грани Вашей поделки с предлагаемым чертежом.
2. Можем воспользоваться Аксиомой о пересечении двух плоскостей: Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. Точки A1 и E1 делят рёбра AB и BC, т.е. точки A1 и E1 принадлежат грани ABC, Точки F и E1 принадлежат рёбрам FB и BС, т.е. точки F и E1 принадлежат грани FBC. Две грани, ABC и FBC имеют одну общую прямую BC.
Ответ:
1) BC
Задача № 6
Сложность 1/5
Задание:
Точки A1 и E1 делят рёбра AB и BC куба ABFEDCGH в отношении 1:3.

Вопрос:
По какой прямой пересекаются плоскости DCE1 и A1BF Варианты ответов:
1) BC
1) HE
1) AB
Решение:
1. Для визуального удлинения одной из сторон сечения можно воспользоваться методом приложения карандаша к уже имеющемуся изделию. Не забудьте, пожалуйста, верно сопоставить грани Вашей поделки с предлагаемым чертежом.
2. Можем воспользоваться Аксиомой о пересечении двух плоскостей: Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. Точки A1 и E1 делят рёбра AB и BC, т.е. точки A1 и E1 принадлежат грани ABC, Точки F и A1 принадлежат рёбрам FB и BA, т.е. точки F и E1 принадлежат грани FBA. Две грани, ABC и FBA имеют одну общую прямую BA.
Ответ:
1) AB
Задача № 7
Сложность 2/5
Задание:

Через какие указанные точки можно провести единственную плоскость. Варианты ответов:
1) FM2G
2) FZ1E
3) AV1G
Решение:
1. Можно рассмотреть сечение красного куба
2. Воспользовавшись Аксиомой: через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна; заметим, что из предложенных вариантом лишь один, AV1G, задает точки не принадлежащие одной прямой.

Ответ:
AV1G
Задача № 8
Сложность 2/5
Задание:

Выберите верные утверждения:
1) C2G1 ⊥ G1F3
2) UT ∥ CF
3) TF3 ∥ C1G1
4) DA ⊥ BF
Ответ:
2) UT ∥ CF
3) TF3 ∥ C1G1
4) DA ⊥ BF
Задача № 9
Сложность 5/5
Задание:
Площадь какого многоугольного сечения больше?

Варианты ответов:
1) у зеленой модели
2) у оранжевой модели
Решение:
1. Наложите два многоугольника друг на друга и оцените разницу визуально.
2. Для оранжевой модели:
Разделим пятиугольник на две фигуры, на треугольник и трапецию.

Выразив, получаем, что площадь пятиугольника равна: 
Для зеленной модели куба – площадь сечения в форме правильного шестиугольника:  где n - число сторон
где n - число сторон
a – длина стороны
Таким образом:
Ответ:
у зеленой модели площадь сечения больше
38,9 см2 (у зеленой модели) > 34,3 см2 (у оранжевой модели)
Автор задач: математик Соколова Александра
посмотреть другие сечения куба можно здесь
Подробная сборка от Алексея Жигулева (youtube-канал Оригами)
© 2011 - 2025 гг. ООО «Многогранники». Все права сохранены.

