Развитие пространственного воображения

0 руб.
0 товар(ов)

Куб Принца Руперта

В выпуске 25 «Волшебных граней» мы обратили взор читателя на то, что разрезая куб плоскостью, мы получаем в точке разреза сечение, имеющее форму многоугольника.
И эта геометрическая форма будет меняться в зависимости от угла наклона плоскости.

Взяв три куба, мы последовательно разрезали их плоскостью, и получили семь разных сечений:
- два правильных треугольника, отличающихся своими размерами;
- квадрат;
- прямоугольник;
- ромб;
- пятиугольник;
- правильный шестиугольник.

Здесь это можно увидеть на видеоролике.

Как вы, наверное, догадываетесь, это далеко не все возможные многоугольники, которые можно получить, рассекая куб.

Но если классические разрезания куба вам показались скучным, то вот история, рассказанная в 1693 году английским математиком Джоном Валлисом.

Принц Руперт Пфальцский поспорил, что в кубе можно вырезать отверстие, достаточно большое, чтобы через него можно было протащить куб такого же размера.

Принц Руперт Пфальцский (нем. Ruprecht) (1619–1682).
Руперт – один из основателей Компании Гудзонова залива и первый ее управляющий. В 1646–1648 Руперт возглавлял английские части в составе французской армии. Кроме того, он был талантливым изобретателем, а также превосходным гравером, внедрившим в Англии технику меццо-тинто.

Итак, что мы имеем? В наличии два одинаковых по размерам куба.

В одном из кубов нужно сделать сквозное отверстие.
Чтобы в это отверстие пролез куб, размер отверстия должен быть подходящего размера.
Какого? Скорее всего, это должно быть отверстие наименьшее по площади. В таком случае размер отверстия будет квадратным и равен площади стороны куба. В такое квадратное отверстие куб пройти сможет.

С формой отверстия мы определились – это квадрат, равный стороне куба.

Теперь попробуем так повернуть второй куб, чтобы внутри первого (зеленого) можно было сделать квадратное отверстие. Сложность задачи состоит в том, чтобы это было внутреннее отверстие, а внешние стенки разрезаемого куба были бы неразрывны.
попытка сделать сечение

Сначала может показаться, что как ни крути куб, отверстие явно не может быть только внутренним и выйдет за грань разрезаемого куба.
Но это предположение будет действовать до тех пор, пока вы не повернёте зеленый куб следующим образом:

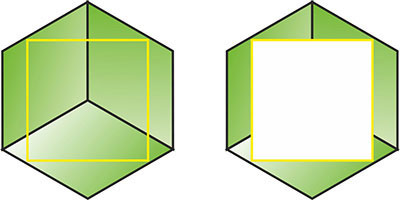
В этом случае мы можем сделать внутри зеленого куба такое отверстие, что в него целиком пройдет жёлтый куб, насквозь.

Джон Валлис доказал, это математически и принц Руперт выиграл свой спор.

Валлис предположил, что такое отверстие будет параллельно пространственной диагонали куба.
сечение принца руперта

Проекция куба на плоскость, перпендикулярная этой диагонали, является правильным шестиугольником, а самое большое отверстие, параллельное диагонали, можно получить, нарисовав наибольший квадрат, который можно вписать в этот шестиугольник.

Модель куба с вырезанным отверстием должна выглядеть следующим образом:

А вот как будет выглядеть ситуация, когда один куб проходит сквозь другой
сечение принца руперта

Примерно через 100 лет голландский математик Питер Ньюланд вычислил, что может быть найдено лучшее решение. Всё дело в том, что физическая модель куба Принца Руперта весьма сложна в изготовлении, так как имеет в четырех точках очень тонкие стенки. Оптимальное решение, предложенное Питером Ньюландом, может быть получено при прорезании отверстия под другим углом, чем пространственная диагональ. Это позволяет увеличить толщину стенок в тонких местах.

P.S.

В логотипе известной программы от компании Майкрософт можно увидеть в чём-то сходную картинку, с кубом у которого вырезана серединка.

Куб Принца Руперта

Принц Руперт Пфальцский поспорил, что в кубе можно вырезать отверстие, достаточно большое, чтобы через него можно было протащить куб такого же размера.

Популярное