Сечения белого куба

Задача № 2

Задание:

Округлите иррациональное число 6√2 до десятых.

Варианты ответов:

1) 7
2) 8,5
3) 12,2
4) невозможно.

Решение:

1. Рассмотрите модель белого цвета, а именно, её среднее сечение, содержащее диагонали двух граней. Посчитайте количество диагоналей единичных квадратов. Каждая диагональ единичного квадрата равна √2. Всего их 6. Следовательно, длина диагонали 6√2. Измерьте эту диагональ линейкой. Полученный результат и является ответом: 8,5 см.

2. Методом подбора узнаем, что 1,414²=1,9994<2, а 1,415²=2,00223>2, таким образом, так как нас просят округлить до десятых, получаем, что √2 ≈1.414. Тогда 6√2=8,484≈8,5

Ответ:

2) 8,5

Задача № 3

Задание:

Найдите расстояние от точки E до прямой FH.

Варианты ответов:
1) 3
2) 3√2
3) 4

Решение:

1. Рассмотрите модель белого цвета, а именно, её среднее сечение, содержащее диагонали двух граней. Проведите еще одну диагональ одной из граней. Так как грани имеют форму квадрата, а диагонали пересекаются под прямым углом, то половина диагонали и будет расстоянием от точки до прямой. Сосчитаем количество диагоналей единичных квадратов. Получим 3√2

2. Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из это точки на прямую. В прямоугольном равнобедренном треугольнике FEH построим высоту EM к гипотенузе. Легко доказать, что EM=FH/2=3√2

Ответ:

2) 3√2

Задача № 4

Задание:

На сколько минут уменьшится время обхода кровельщика по периметру крыши, если сделать помост на высоте 2/3 от верхнего гребня? Если крыша покрывает здание с периметром почти в 29 м., а именно 12⋅(√2+1)м, а возможная скорость кровельщика не более 0,4 м/с.

Варианты ответов: 

1) 1 минута,т.е. 60 секунд
2) не изменится
3) 14 секунд.

Решение:

1. Рассмотрев белую модель куба, заметим, что большее сечение имеет периметр состоящий из 12 диагоналей единичных квадратов и 12 сторон единичных квадратов. А периметр меньшего сечения лишь из 12 сторон единичных квадратов, но лишь из 8 диагоналей. Таким образом, отметим, что разница периметров равна 4 диагоналям единичных квадратов. Диагональ единичного квадрата, по теореме Пифагора, равна √2. Это означает, что путь уменьшится на 4⋅√2≈5,66. А время, соответственно, на 4⋅√2:0,4≈14 секунд

2. Построив два прямоугольных сечения куба с ребром равным 6 единичным отрезкам, так как P=12⋅(√2+1)=12√2+12=2⋅(6√2+6), найдем периметры указанных сечений и рассчитаем по формуле T=S/V время.

Ответ:

3) 14

Задача № 5

Задание:

Муравьи смогли прогрызть кубик сахара, аналогичный белой модели куба. Благодаря чему, кубик сахара распался на 3 кусочка. Какое минимальное количество муравьев необходимо на каждый кусочек, если каждый муравей может поднять массу, превышающую массу самого муравья в 50 раз. При этом, известно, что самые легкие муравьи — фараоновы, всем известные домашние вредители, и некоторые виды тропических муравьев, такие же мелкие. Масса муравья из касты рабочих у этих видов составляет 1-2 миллиграмма (т.е 0,01 гр). А масса 1м³ сахара равен 1600 кг.
Подсказка: попробуйте угадать ответ, основываясь на ощущениях объема данных частей. Во сколько раз каждая часть больше по объему?

Варианты ответов:

1) 250, 250 и 500
2) 112, 224 и 336
3) 154, 346, 538
4) 154, 192, 346

Решение 1:

Для подсчета количества муравьев, необходимо понять, каков объем каждой части. Обратившись к соответствующей модели, произведем следующие измерения:
Первым многогранником рассмотрим наименьший из трех. Его объем будем искать интегрированием (не стоит бояться этого слова, все очень просто). Сперва измерим площадь торцевого треугольника ELK. Имея модель в руках, ее можно просто посчитать по квадратикам (не имея данной модели, так же возможно выполнить подсчет, но необходимо воспользоваться соответствующей формулой площади треугольника). Получаем 8 единичных квадратов. Каждый квадрат при этом имеет площадь равную 1 см² или 100 мм². То есть, S=800 мм². Далее, рассмотрим, что грань EKJ имеет длину 6 единичных квадратов (KJ = 6 ед). То есть, если начать отрезать слои треугольной формы, двигаясь вдоль KJ, и толщиной в 1 миллиметр, то у нас получится 6⋅10=60 таких слоев. Осталось выполнить последнее умножение: 800 ⋅ 60 = 48000 мм³ = 48 см³.
Теперь разберем величины массы сахара. В условии задачи указано, что вес 1 м³ сахара равен 1600 кг. 1 м³ означает, что у вас рассматривается куб с ребром 1 м. Мы же получили объем кусочка в см³. Перевод единиц не вызовет затруднений, если вспомнить, что в 1 метре содержится 100 см. Т.е. 1 м³ = 100³ см³ = 1 000 000 см³ . Тогда, чтобы узнать, вес 1 см³, необходимо вес 1м³ разделить на 1 000 000, то есть 1600 кг = 1 600 000 гр : 1 000 000 = 1,6 гр.
Это означает, что рассмотренный нами кусочек имеет массу 48⋅1,6=76,8 гр. И его смогут поднять: 76,8:(0,01⋅50)=153,6 муравья. Но муравьев лучше не рубить на части, поэтому лучше с запасом взять 154 муравья.
Аналогичные расчеты проведем и для большего кусочка:
1800⋅60 : 1000 = 108 см³.
Или проще: 6³ : 2 = 108 см³
Тогда для подсчета количества муравьев:
108⋅1,6 : (0,01⋅50) = 345, 6
То есть, 346 муравьев.
Чтобы найти объем средней части нашего куба, достаточного из общего объема вычесть уже найденные два объема:
6³ = 216 - 108 - 48 = 60
Тогда количество муравьев:
60 ⋅ 1,6 : (0,01 ⋅ 50) = 192
Количество муравьев, конечно же, поражает. Но и кусочек сахара в данном примере взят довольно большим. Но его модель помогает разобраться и в более реальной ситуации. В том числе становится понятно то, что наименьший кусов почти в 2 раза меньше среднего

Решение 2:

В основном школьном курсе стереометрии, в разделе пирамид, мы не найдем формулы для вычисления объема «крыши», объема маленького кусочка сахара. Однако, если поставить эту «крышу» на торец, то получится призма с верхним и нижним основаниями в форме треугольников. Тогда, вспомнив формулу нахождения объема треугольной призмы, мы с Вами легко поймем, что, умножив площадь треугольника на высоту этой призмы, получим ее объем: 18 ⋅ 6 = 108 см³. Если же формула никак не вспоминается или не была пройдена, то тоже не беда. Ведь в школе прекрасно объясняется умение делить объемы. И если, общий объем куба 6³=216 см³, то его половина равна 6³ : 2 = 216 : 2 = 108 см³. Так находится объем большего многогранника их трех имеющихся. Дальше хотелось бы воспользоваться понятием коэффииента подобия. Ведь, мы знаем с вами, что отношение периметров подобных фигур равно коэффициенту подобия (k), отношение площадей равное коэффициенту подобия в квадрате (k²), а объемы - k³. Но, к сожалению, данные кусочки не подобны (подумайте самостоятельно, почему). Поэтому для подсчета объема самого маленького кусочка, мы достроим его до параллелепипеда с ребрами 6 и 4,4. Его объем найти легко: 6 ⋅ 4 ⋅ 4 = 96 см³. И так как, наш искомый многогранник является его половиной, то 96 : 2 = 48 см³
Далее займемся вычитаем объемов. Из общего вычтем найденные части:
216 - 108 - 48 = 60
И получим, что объем средней части равен 60 см³
Теперь остается посчитать количество муравьев, как в предыдущем примере решения.

Ответ:

3) 154, 192, 346

Задача № 6

Задание:

Крыша государственного исторического музея имеет схожую форму со средней частью модели белого цвета. И если для модели нашего куба изменения не сильно повлияют на массу изделия, то изменение в пропорции крыши музея может привести к ее обрушению. Данные задачи решаются еще на этапе проектирования. Давайте и мы попробуем узнать, на какую площадь увеличится средняя часть заготовки белого цвета, если к ней приклеить первую, наименьшую часть .

*Подсчет площади применяется при подсчетах расходного материала для настила кровли. Подсказка: Чтобы узнать площадь малой части, достаточно посчитать количество квадратов. Обратите внимание, что в сумме получается целое число.

Варианты ответов: 

1) на 32 ед²
2) на 100√2 ед²
3) 64 ед²

Ответ:

3) 64 ед²

Задача № 7

Задание:

Насыпь шоссейной дороги имеет в верхней части ширину 40√2 м. Какова ширина насыпи в нижней ее части, если угол наклона откосов равен 45°, а высота 10√2 м?

Варианты ответов:

1) 60√2
2) 50√2
3) 100√2

Решение 1:

Рассмотрите белую модель. Найдите соответствующую деталь. Сосчитайте количество диагоналей единичного куба.

Решение 2:

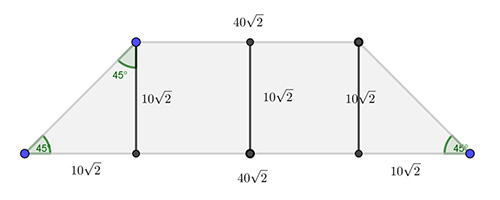
Ответ:

1) 60√2